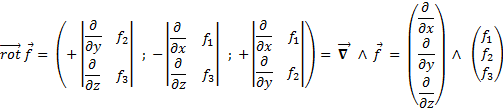Les Opérateurs Différentiels.
Approche historique.
Nabla. [CajoV2] p 135
Le mathématicien irlandais HAMILTON William Rowan (1805-1865) introduit l'opérateur Nabla en 1853 dans ses Lectures on Quaternions. Cependant le d rond ∂, de cet opérateur (indiquant les dérivées partielles), n'apparait que chez A McAulay dans son Octonions en 1898.
Le mathématicien et physicien écossais TAIT Peter Guthrie (1831 - 1901) développera l'utilisation de l'opérateur Nabla dans dans ses Elementary Treatise on Quaternions (1867), et Introduction to Quaternions (1873).
HAMILTON utilise le symbole et TAIT lui préfère le Δ inversé dans An Elementary Treatise on Quaternions (1867).
Le symbole Δ inversé pour désigner cet opérateur est appelé Nabla par le mathématicien anglais HEAVISIDE Oliver (1850-1925).
Gradient. [CajoV2] p 135
Le symbole grad est utilisé par l'écossais James Clerk MAXWELL (1831 -1879), et les allemands RIEMANN (1826-1866) et WEBER Heinrich (1842-1913).
Divergence. [CajoV2] p 135
The terme DIVERGENCE fut introduit par William Kingdon CLIFFORD (1845-1879) dans son Elements of Dynamic (1878).
L'opérateur divergence est utilisé par GIBBS (1839 - 1903) et HEAVISIDE Oliver (1850-1925) avec l'opérateur Nabla.
Rotationnel. (Curl en anglais) [CajoV2] p 135
En 1873, James Clerk MAXWELL (1831 -1879) introduit dans A Treatise on Electricity and Magnetism l'opérateur rotationnel qu'il nomme curl. Puis E. B. WILSON dans Vector Analysis (1901) propose la notation du rotationnel avec Nabla.
Cours sur les opérateurs différentiels. (Version PDF)
1 – Pour f champ scalaire : Nabla, Gradient et Laplacien.
Soit f une application de U ouvert de IRn à valeur dans IR
Opérateur Nabla.
Gradient de f. Pour f fonction C1(U)
Laplacien : Pour f C²(U)
2 – Champ de vecteur : Divergence et rotationnel.
Application f de U ouvert de IR3 (resp. IR²) , à valeur dans IR3 (resp. IR²) , f = (f1,f2,f3) avec les fi C1(U)
Divergence :
Rotationnel :
3 - Propriétés des opérateurs différentiels.
3a : Linéarité.
Les opérateurs gradient, rotationnel et divergence sont linéaires.3b : Produits. (Sous réserves d'existence)
3c : Composées
4 – Potentiel scalaire.
On considère un champ de vecteurs F de U⊂ IR3 dans IR3, de classe C1.
F dérive d’un potentiel scalaire (ou admet un potentiel scalaire)
si il existe un champ scalaire f de U⊂IR3 → IR , de classe C1 sur U, tel que :
Théorème.
1°) Si dérive F d’un potentiel scalaire alors :2°) Si
et si U est étoilé, alors F dérive d’un potentiel scalaireRemarque : se démontre avec le théorème de Poincaré.