PYTHAGORE de Samos
PYTHAGORE de Samos
Naissance: vers 569 av.J-C. à Samos, Ionie - Mort: vers 475 av.J.-C. à Crotone ?
Sa vie
D'une génération plus jeune que le mathgématicienThalès, le célèbre Pythagore aurait vécu dans la seconde moitié du 6ème siècle av. J. C.
Bien sur, peu de choses sont avérées, il faut plutôt lire l'histoire ci-dessous comme un joli conte. Quelques épistémologues avertis vont même jusqu'à voir en Pythagore un nom générique, (c'est un nom courant à l'époque), désignant un groupe de personnes.
Cependant Euclide le cite ainsi que quelques historiens de l'antiquité, alors..... rêvons.
1. Pythagore et ses voyages formateurs
Né à Samos (Grèce), Pythagore avait 18 ans lorsqu'il participa aux Jeux olympique et remporta toutes les compétitions de pugilat (sport de l' antiquité comparable à la boxe, mais dans lequel les combattants portaient au poing un gantelet garni de fer ou de plomb, la ceste).
Par la suite, il décida de voyager.
- En Ionie toute proche, il passa quelques années auprès de Thalès et de son élève Anaximandre (v. 610 BC - v. 546 BC).
- Puis en Syrie, il séjourna avec les sages Vénitiens qui l' initièrent aux mystères de Byblos.
- Puis au mont Carmel, dans le Liban d' aujourd'hui.
- De là, il s' embarqua pour l' Égypte et y resta 20 années.
Lorsque les Perses envahirent le pays, il se serait retrouvé prisonnier et emmené à Babylone. Durant 12 années, il y acquiert l' immense savoir des scribes et mages babyloniens.
Pythagore a acquis ses connaissances mathématiques au cours de ses voyages.
On avance même qu'il aurait été jusqu'en Inde et en Bretagne, mais il est plus certain qu 'il ait recueilli plusieurs de ses techniques et de ses outils mathématiques auprès des Égyptiens et des Babyloniens.
Ces deux peuples avaient dépassé les limites de l' arithmétique élémentaire et étaient capables d'effectuer des calculs complexes : résolution d' équations du second degré (c. f. histoire des équations), système de numération évolué (c. f. numération babylonienne).
Cependant, ils considéraient les mathématiques comme un simple instrument utile pour résoudre des problèmes pratiques, ainsi, les motifs de la recherche de certaines règles de géométrie étaient d' établir les limites des champs recouverts lors des crues du Nil (le mot géométrie signifie "mesure de la terre").
Pythagore s' avisa que les Égyptiens et les Babyloniens effectuaient chaque calcul selon des recettes qu 'ils se transmettaient de génération en génération, sans en analyser la logique.
2. Le retour de Pythagore à Samos
Au terme d' une quarantaine (?!) années de voyages, Pythagore avait assimilé toutes les règles mathématiques du monde connu. Il partit pour son île natale de Samos en mer Égée, avec l' intention de fonder une école consacrée à la philosophie et aux règles mathématiques découvertes.
En son absence, le tyran Polycrate (535 av. JC- 515 av. JC) avait changé l' île ; jadis libérale, elle était devenue intolérante et conservatrice. Pythagore refusa l' invitation de Polycrate (535 av. JC- 515 av. JC) à sa cour et quitta la ville pour s' installer dans une caverne.
L' isolement lui pesa et il finit par proposer de l'argent à un garçon (dont le nom aurait été également Pythagore selon quelques historiens) pour qu'il devînt son élève.
Du maître au disciple.
Pythagore le maître, payait Pythagore l'élève, 3 oboles par leçon et le premier se rendit compte de l'enthousiasme manifesté par le garçon au bout de quelques semaines. Pour mesurer son succès, Pythagore prétendit manquer de moyens pour continuer, ainsi et le garçon proposa de payer pour son éducation plutôt que de l'interrompre.
L'élève était devenu disciple. Ce fut malheureusement la seule conversion effectuée par Pythagore à Samos. Il y eut bien une école connue sous le nom de l'Hémicycle de Pythagore mais les notions de réforme sociale y étant enseignées conduisirent Pythagore à fuir Samos en compagnie de sa mère et de son unique disciple.
3. Pythagore à Crotone : La fraternité pythagoricienne
3a. La naissance de la Fraternité pythagoricienne et son fonctionnement.
Pythagore fit voile pour l'Italie du sud (qui faisait alors partie de la Grande Grèce), débarqua à Sybaris (la ville de tous les plaisirs) et s'installa à Crotone.
Il eut la chance d'y trouver Milon, le protecteur idéal, l'homme le plus riche de la ville et l'un des plus forts de Grèce (couronné 12 fois aux Jeux olympiques et pythiques).
Dans la sécurité de sa nouvelle installation, Pythagore fonda la Fraternité pythagoricienne, un groupe (ou une secte, sans doute la première) qui compta 218 (certains avance le nombre de 600..) pythagoriciens
3b. Les pythagoriciens célèbres.
Parmi les pythagoriciens, outre le maitre on compte, Philolaos (5ème av. J.-C.), Archytas (428-347 av. J.-C.), Hippase de Métaponte (5ème av. J.-C.), Hippocrate de Chios ( 470 av.JC - 410 av. JC), Théodore de Cyrène (470 av. JC - 420 av. JC), Philolaos (5e av. JC) (Pythagoricien Astronome et spécialiste de la cosmogonie, il avait imaginé un système du monde où la terre et les autres planètes tournaient sur elles-mêmes ET autour d'un feu central !!), Architas de Tarente.
Cette école pythagoricienne dura près de 150 ans mais tous ne furent pas mathématiciens, loin s'en faut.
L'école pythagoricienne accueillait aussi des femmes, comme élèves et comme professeurs.
Le philosophe JAMBLIQUE (250 à Chalcis (Syrie) - 325) dans son ouvrage, la Vie de Pythagore, répertorie 17 pythagoriciennes remarquables, filles ou femmes de pythagoriciens.
Timycha, épouse de Myllias de Crotone ; Philtys, fille de Theophrios de Crotone ; Théano, épouse de Brontinos de Métaponte ou de Pythagore lui même....
Selon certains, Théano était la fille d'un philosophe et médecin crétois nommé Pythonax (admirateur de Pythagore). Disciple de l'école, elle serait devenue l'épouse du maître Pythagore.
3c. Le fonctionnement de la fraternité.
Les tests d'entrée.
Lorsqu'il adhérait à la fraternité, chaque disciple devait faire don de toutes ses possessions à un fond commun. A son départ, il recevait le double de ce qu'il avait offert en arrivant et l'on érigeait une stèle en sa mémoire.
Pythagore se chargeait de tester les candidats. Il commençait par observer si le postulant était capable de "tenir sa langue", c'est le terme qu'il employait.
Pouvait-il se taire et garder pour lui tout ce qu'il avait entendu durant les séances d'enseignement ?
La salle de cours était séparée en deux par un rideau.
Pythagore se trouvait d'un côté, les postulants de l'autre ; ils n'avaient accès qu'à un enseignement oral. L'épreuve durait 5 ans.
Ce rideau avait une extrême importance dans la vie de l'école pythagoricienne. Les membres de l'école étaient répartis en 2 catégories. Du côté de la salle où se trouvait Pythagore et pour le reste de leur vie, les ésotériques, et de l'autre les exotériques.
Le savoir préservé.
Les textes des pythagoriciens étaient eux aussi soumis au secret ; rédigés dans un langage à double sens, ils n'étaient réellement accessibles que par les initiés. Ils parlaient de sumbola(symboles) et d'ainigmata (énigmes).
La plupart des connaissances se transmettaient de bouches à oreilles, cela donnait lieu à une deuxième séparation.
Il y avait :
- les "acousmaticiens", ou akoustiskoï (de akousmata, les choses entendues) à qui l'on transmettait les résultats mais pas les démonstrations,
- et les "mathématiciens", ou mathematikoï (de mathema, la science, c'est à dire chez les grecs, toute la connaissance) à qui l'on transmettait les résultats et les démonstrations.
Hippase (v. 500 av. JC) (qui inventa dit-on la moyenne harmonique), fut l'un des premiers pythagoriciens ; il était le chef des "acousmaticiens", les candidats à l'initiation, tandis que Pythagore dirigeait les "mathématiciens", les initiés.
Tous les membres de la fraternité devaient donc exercer leur mémoire. Chaque matin, ils devaient se remémorer les événements de la veille.
3d. Les fondements la Fraternité pythagoricienne : "TOUT EST NOMBRE".

Avec les pythagoriciens, l'univers des mathématiques s'est agrandi.
Ils ont introduit la musique et la mécanique.
Leur vision mystique des nombres ne les a pas empêchés de fonder l'arithmétique comme la science des nombres. C'est à eux que l'on doit les premières véritables démonstrations de l'Histoire.
Pour Pythagore, "tout est nombre" (on entend par nombre un entier ou une fraction), c'est dans la musique qu'il les dénicha pour la 1ère fois.
En effet, la musique était alors une partie intégrante de la science et des mathématiques. L'harmonie était la mise en son de rapports numériques.
L'ordre des cieux s'exprimait par une gamme musicale. La musique des sphères.
Pour dire cela , Pythagore inventa le mot "cosmos" (mot gr. ordre), "Le bon ordre et la beauté".
Et l'histoire du monde se raconta comme la lutte du cosmos contre le chaos.
Donner à la connaissance de la nature un fondement numérique, tel était le projet des pythagoriciens.
En outre, peu après avoir fondé la Fraternité, Pythagore inventa le mot philosophe.
Alors qu'il assistait aux Jeux olympiques, Léon, prince de Phlius, demanda à Pythagore comment il se définissait. "Je suis un philosophe ", répondit-il.
« La vie, prince Léon, peut être comparée à ces jeux publics, car dans le vaste public assemblé ici se trouvent des gens qui sont attirés par le gain, d'autres par les espoirs de la renommée et de la gloire. Mais il y en a aussi qui sont venus pour observer et comprendre tout ce qui se passe ici.
Il en va de même avec la vie. Certains sont menés par l'amour et la richesse, d'autres guidés aveuglement par la soif insensée de puissance et de domination, mais l'homme le plus noble se consacre à la découverte du sens et du but de la vie. Il cherche à découvrir les secrets de la nature. C'est celui que j'appelle un philosophe car , bien qu"aucun homme ne soit sage à tous égards, il peut aimer la sagesse comme clef des secrets de la nature. »
4. Les découvertes de la Fraternité pythagoricienne
4.a. Le théorème de Pythagore.
Le fameux théorème de Pythagore, qu' Euclide (3e av. JC) démontre dans ses "Éléments" est bien sur la plus célèbre "découverte" qu'on leur attribue.
Il faut préciser ce théorème de Pythagore.
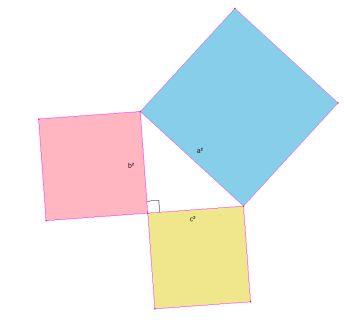
« Dans un triangle rectangle, la carré de l'hypoténuse est égal à la somme des carrés des 2 autres côtés.»
Ici a² = b² + c², c'est à dire que l'aire du carré de côté a construit sur l'hypoténuse du triangle rectangle, est égale à la somme des aires des deux autres carrées.
Cependant, des tablettes cunéiformes attestent de la connaissance par les babyloniens de ce théorème. Il était en fait déjà connu des chinois et des Babyloniens, 1 000 ans auparavant.
Par contre, ces derniers n'avaient pas conscience que le théorème valait pour tous les triangles rectangles.
La découverte, que ce théorème s'applique à tous les triangles rectangles, fut tellement sensationnelle que 100 bœufs furent sacrifiés en témoignage de gratitude à l'égard des dieux (on appelait cela une hécatombe).
La première démonstration.
Nous devons la première démonstration attestée de la propriété de Pythagore à Euclide (3e av. JC).
Il s'agit de la proposition 47 du 1er livre des Éléments et de la réciproque, proposition 48, qui terminent ce 1er livre.
Ce théorème compte 370 démonstrations (d'Euclide, des savants chinois, du 20e président des États-Unis, James Abram Garfield en 1876......etc..) faisables en classe de seconde.
Il n'existe aucune preuve que les pythagoriciens en connaissaient une démonstration,et les historiens des sciences pensent généralement que non, bien qu'ils aient conscience de la nécessité d'une démonstration.
Compléments : => théorème de Pythagore
4.b. La mystique des nombres.
Pour les pythagoriciens, TOUT EST NOMBRE. Ils associent chaque nombre (entier) à une figure géométrique.
Pour les pythagoriciens, les l'Univers des Nombres se compose de :
- La monade : le nombre un,
- La dyade : le nombre deux, premier nombre paire et féminin,
- La triade : le premier nombre impair et masculin,..
- La décade : qui représente la somme des points contenus dans le Tétraktys, symbole ésotérique pour les membres de la fraternité.
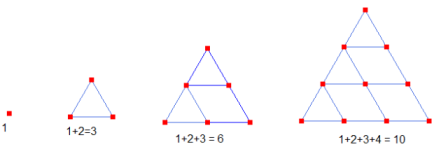
Les pythagoriciens ont étudié cette figure considérée comme mythique, le Tétraktys, La Décade.
Le Tétraktys est "une image figurée de la structure du monde".
La figure classique est celle d'un triangle de quatre lignes tel que 1 + 2 + 3 + 4 = 10 points ou cailloux.
Il représente l'être parfait car il contient toute les dimensions de l'espace : 1 (le point), 2 (la ligne), 3 (la surface) et 4 (le solide). Il est la somme des 4 premiers nombres : 1+2+3+4 = 10.
On raconte qu'ils lui auraient même adressé une prière :
« Bénis-nous, nombre divin, toi qui as engendré les dieux et les hommes ! O sainte, sainte Tétraktys ! toi qui contiens la racine et la source du flux éternel de la création ! Car le nombre divin débute par l'unité pure et profonde et atteint ensuite le quatre sacré; ensuite il engendre la mère de tout, qui relie tout, le premier-né, celui qui ne dévie jamais, qui ne se lasse jamais, le Dix sacré, qui détient la clef de toutes choses. »
4.c. L'étude des nombres, l'arithmétique.
Les pythagoriciens s'intéressèrent aux nombres entiers, aux nombres parfaits (somme de leur diviseurs propres), aux nombres "excessifs", "imparfaits". (cf. les nombres remarquables).
Ils tentèrent de trouver des nombres "un peu excessifs", c'est à dire dont la somme des diviseurs était supérieure d'une unité à ces nombres. Ils n'y arrivèrent pas et, de nos jours, nous restons incapables de prouver qu'il n'en existe pas !!!
4.d. La première crise de l'histoire des mathématiques.
La découverte des nombres irrationnels, c'est à dire des nombres que l'on ne peut pas écrire sous le forme d'une fraction, est généralement attribuée aux pythagoriciens.
Les pythagoriciens démontrèrent l'irrationalité de √2 : Cette découverte serait due à Hippase de Métaponte qui, après avoir enfreint les règles de la fraternité en divulguant sa découverte, péri dans un naufrage.
Cette découverte débouche sur la première crise de l'histoire des mathématiques.
En effet, les pythagoriciens pour qui tout est nombre (ils entendent par là, tout est entier ou rationnel) ne peuvent supporter l'apparition de nouvelles entités numériques. Toute leur vision du monde en est changée.
La diagonale d'un carré de côté 1 est √2, est une grandeur incommensurable, inexprimable, alogon (indicible, privé de raison commune), puisqu'elle ne peut pas s'écrire sous la forme d'une fraction.
C'est une découverte très dure pour la fraternité, puisqu'un de ses fondements, le lien capital entre les nombres et les grandeurs, fut brutalement rompu.
4.e. En géométrie.
On a vu que l'arithmétique des pythagoriciens est géométrique, puisqu'à chaque nombre ils associent une figure.
Ils démontrèrent aussi que la somme des mesures des angles d'un triangle fait 180°.
5. La mort de Pythagore
Les nouvelles des succès de la Fraternité se répandirent mais la teneur des découvertes restait jalousement gardée. Il y avait beaucoup de candidats au saint du saint du savoir, mais n'étaient acceptés que les esprits les plus brillants.
L'un des recalés fut Cylon. Il s'en offensa et, comme nous allons le voir, il se vengea 20 ans plus tard.
Lors de la 67e Olympiade, en 510 avant notre ère, une révolte éclata dans la cité voisine de Sybaris. Telys, le meneur et héros de la révolte, entreprit des persécutions contre les partisans du gouvernement précédent, ce qui poussa plusieurs d'entre eux à se réfugier à Crotone.
Telys demanda que les traîtres fussent expulsés vers Sybaris pour y subir leur châtiment, mais Milon et Pythagore convainquirent les citoyens de Crotone de résister au tyran.
Après 70 jours de guerre, Milon et ses 100 000 citoyens armés remporta la victoire face à Telys et ses 300 000 hommes.
Cependant, après la guerre, Crotone se divisa sur la partage du butin. Craignant que les terres fussent données aux pythagoriciens, le peuple de Crotone fronda. Les choses s'envenimèrent quand Cylon, se présenta comme la voie du peuple. Attisant la peur et l'envie de la foule, il lança la populace à l'assaut et détruisit la plus brillante école de mathématiques jamais vue. Les bâtiments furent incendiés et Pythagore et plusieurs de ses disciples y périrent.
Après la mort de son fondateur, la Fraternité quitta Crotone pour d'autres cités de la Grande Grèce mais la persécution continua et plusieurs pythagoriciens durent chercher refuge dans des contrées étrangères. Les disciples essaimèrent donc leur évangile mathématique au travers du monde antique.
Bibliographie
- [Esco] : Jean-Pierre ESCOFIER, Théorie de Gallois, Masson, Paris, 1997. Page 12
- [Guedj1] : Denis GUEDJ, Le théorème du perroquet, Seuil (*)
- [Singh ] : Simon Singh, Le dernier théorème de Fermat, JC Jattès.
- [TanHs30] : Tangente, Histoire des mathématiques de l'Antiquité à l'an Mil, HS n°30, Pole, Paris, 2007.