 ÉRATOSTHÈNE de Cyrène
ÉRATOSTHÈNE de Cyrène
Cyrène vers 276 - Alexandrie vers 194 av. J.-C.
1. Ératosthène de Cyrène.
Ératosthène est un astronome, philosophe, géographe et mathématicien, né à Cyrène, une ancienne ville grecque en actuelle Libye. Cette ville porte maintenant le nom de Shahhat.
Après avoir suivi des études dans sa ville natale, il aurait été l'élève du poète Callimaque de Cyrène (vers 305 - 240 av. J.-C.) à Alexandrie.
Vers l'âge de 20 ans, Ératosthène s'installe à Athènes et y fréquente Ariston et Arcésilas, des élèves de Platon, ainsi que des stoïciens.
Sa notoriété devient telle que le souverain Lagide Ptolémée III Évergète le fait venir à Alexandrie, pour être précepteur de son fils, le futur Ptolémée IV Philopatôr et diriger la grande bibliothèque..
La ville d'Alexandrie, fondée en -331 par Alexandre le Grand, est alors à son apogée. Dans le centre culturel et intellectuel du monde antique, Démétrios de Phalère (mort en 280 av. JC) , a fondé il y a quelques années, la plus grande bibliothèque de l'antiquité. Elle regroupe plus de 400 000 volumes (certains avancent le nombres fabuleux de 700 000) et attirent les plus grands esprits de l'époque.
2. Ératosthène bibliothécaire.
Autre nouveauté et non des moindres : le poste de bibliothécaire est créé.
A l'origine, cet homme ne devait pas être plus qu'un précepteur, mais la Bibliothèque grandit et il devient nécessaire de trouver une personne de référence, capable de s'approprier le lieu, de classifier, de guider les recherches.
Pour Ptolémée III, le nom de l'érudit Ératosthène s'impose alors à ce poste et, de 235 av. J.-C. à sa mort, il devient le troisième conservateur de la fameuse Bibliothèque d'Alexandrie.
Il y édite notamment un ouvrage resté célèbre, un traité d'Archimède intitulé les Éphodiques ou De la méthode.
3. Ératosthène historien et astronome.
En histoire, Ératosthène propose une méthode de classification des évènements historiques.
Il élaboration un système chronologique permettant de dater les événements importants survenus depuis la guerre de Troie, facilitant ainsi la distinction entre les légendes et les faits historiques.
Astronome aussi, certains historiens lui attribuent la création d'un catalogue classifiant 675 étoiles. Il aurait aussi démontré l'inclinaison de l'écliptique sur l'équateur et fixer cette inclinaison à 23° 51. Ératosthène participa en outre à la construction du premier observatoire astronomique.
4. Ératosthène, le premier géographe de l'histoire.
Son savoir pluridisciplinaire lui permet d'envisager une géographie empreinte de mathématique et d'astronomie.
Il rassemble toutes les mesures établies pour rénover la cartographie de l'époque et conçoit une véritable carte du monde connu, c'est à dire du bassin méditerranéen, que l'on nomme écoumène.
L'écoumène est une notion géographique pour désigner l'ensemble des terres habitées ou exploitées par l'Homme.
Il effectue cela avec une remarquable précision pour l'époque. Il est de ce fait considéré comme le premier géographe de l'histoire.
Il propose de diviser la Terre en zones différenciées par la longueur du plus long jour de l'année, les "climats".
Ératosthène décrivait le globe terrestre en cinq zones parallèles : la canicule, bande centrée sur l'équateur, deux calottes polaires, une à chacun des pôles, et deux zones tempérées, comprises entre la canicule et les calottes polaires.
Il aurait aussi donné 47°42' comme mesure de l'arc de méridien compris entre les tropiques du cancer et du capricorne extraordinairement proche de la mesure admise aujourd'hui, à savoir 47°40'.
Il est en cela un précurseur de l'oeuvre de Claude Ptolémée (90 - 168 après J.-C.), et de sa célèbre carte du monde, Imago mundi, que restera la référence de représentation de la Terre durant des siècles.
Notons que c'est à Ératosthène que l'on attribue l'origine du mot géographie.
5. Ératosthène et le calcul de la circonférence de la terre.
Ératosthène et aussi célèbre pour son astucieux calcul de la circonférence de la terre.
Si les résultats obtenus par le savant Ératosthène suscitent bien des interrogations quant à leur (trop ?) remarquable précision, il n'en reste pas moins que la méthode utilisée reste fort ingénieuse.
- Position du problème.
Ératosthène part du constat suivant.
Dans la vile de Syène, au midi solaire local, lors du solstice d'été (le 21 juin), un bâton (ou gnomon) planté verticalement n'a pas d'ombre (ou presque). Ératosthène avait en fait remarqué qu'il ni avait pas d'ombre dans un des puits de la ville à cet instant.
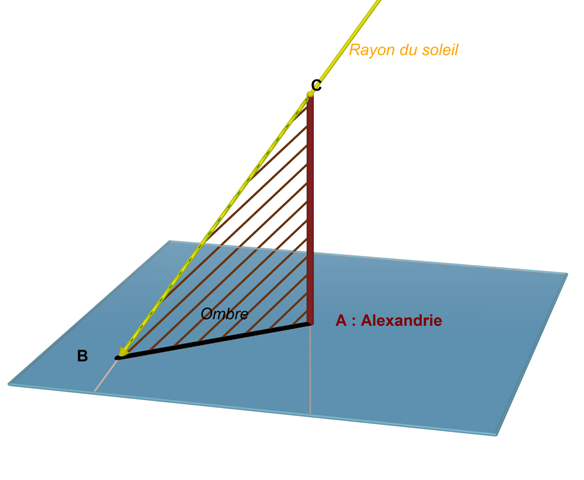 Au même moment, à Alexandrie, on peut mesurer l'ombre [AB] formée par un obélisque [AC] sur le sol.
Au même moment, à Alexandrie, on peut mesurer l'ombre [AB] formée par un obélisque [AC] sur le sol.
Alors, nous pouvons en déduire une mesure de l'angle BCA.
- La mesure de l'angle ACB.
L'œuvre d'Ératosthène a pratiquement disparu, et même si l'astronome grec CLÉOMÈDE (1er siècle), les historiens STRABON (vers 57 av. J.-C., mort entre 21 et 25 ap. J.-C.) et PLINE l'Ancien (23 - 79 ap. J.-C.) relatent l'histoire de cette mesure, personne ne peut affirmer avec exactitude comment Ératosthène a mesuré l'angle à Alexandrie.
On trouve souvent dans la littérature les valeurs de AC = 50 coudées pour l'Obélisque, et de AB = 6 coudées 1/3 pour l'ombre.
Les relations trigonométriques dans le triangle rectangle ABC permettent de donner une approximation de la mesure de l'angle ACB.
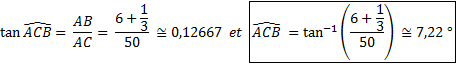
On a donc la configuration suivante :
- La mesure de la circonférence de la Terre.
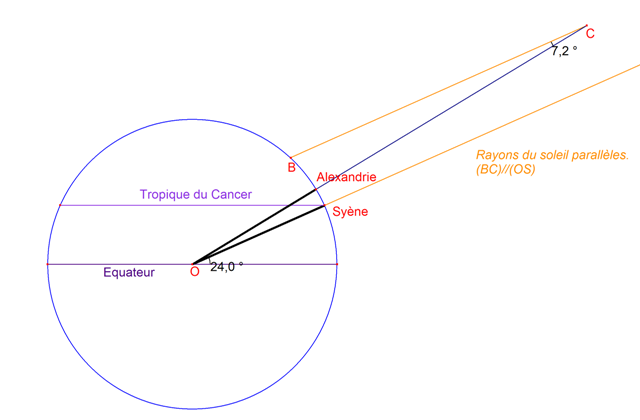
Cette mesure établie, il ne reste plus qu'à constater que les angles BCA et AOS sont de même mesure si l'on considère que les rayons du soleil (SO) et (CB) sont parallèles.
Pour Ératosthène, il ne reste plus alors qu'à calculer la distance entre les villes de Syène et d'Alexandrie. Pour cela requit l'aide d'un bématiste, c'est à dire d'un arpenteur de l'Egypte antique dont la charge était de mesurer des distances. Le bématiste utilisait une méthode simple, il comptait le nombre de pas (bêma) d'un chameau lors du voyage entre deux points. Le chameau étant réputé pour avoir une marche régulière, les calculs étaient d'une précision assez étonnante.
Le bématiste lui fournit donc une mesure de 5 000 stades entre Alexandrie et Syène, soit environ 800 km ce qui est très proche de la réalité.
Ensuite à l'aide d'une simple règle de trois (ou proportionnalité) on obtient facilement :
Si 800 km correspondent à 7,2°, alors un tour complet soit 360° correspond à :
$$\frac{800 \times 360}{7,2}=40~000~km$$
Remarquable, quand on sait que la valeur retenue de nos jours est à l'Equateur d'environ 40 075, 017 km et, en passant par les pôles, de 40 007,864 km.
6. Ératosthène mathématicien, le crible d'Ératosthène.
Dans son œuvre principale « Platonicus », Eratosthène le mathématicien, présente des définitions de géométrie, d'arithmétique et traite aussi d'autres domaines telles que la philosophie ou la musique.
On y trouve par exemple le principe du Mésolabe qui permet d'obtenir une relation de proportionnalité par utilisations réitérées du théorème de Thalès.
Ératosthène reste surtout célèbre en mathématique pour avoir fourni une méthode de recherche des nombres premiers, c'est à dire des nombres (entiers supérieurs ou égaux à 2) qui ne sont divisibles que par 1 et par eux même.
⇒ Pour en savoir plus sur ce crible, visitez la page : Crible d'Eratosthène.
7. La mort d'Ératosthène et conclusion.
Ératosthène devint aveugle à la fin de sa vie. On raconte qu'il préféra se donner la mort (en se laissant mourir de faim) " ne pouvant plus admirer les étoiles " !
Il est amusant de constater que son domaine de notoriété dépend en fait, de la formation de la personne qui vous parlera de lui. Un professeur de mathématiques le qualifiera de mathématicien (mesure de la circonférence de la terre, crible), un professeur d'histoire-géographie, d'historien ou de premier géographe.
Terminons par une petite anecdote.
Eratosthène, le brillant savant, était aussi un athlète, ce qui lui valu le surnom de Pentathlos.
Ses élèves lui auraient aussi donné le surnom de béta, β.
Pourquoi cela ? Parce que doué dans de nombreuses disciplines, il n'était le meilleur dans aucune ou juste pour indiquer la numérotation de sa classe de cours.
Bibliographie.
- [DaDaPe] : A.DAHAN-DALMEDICO/J.PEIFFER, Une histoire des mathématiques, Seuil, Paris, 1986.
- [HaSu] : B. Hauchecorne et D. Surateau, Des mathématiciens de A à Z, Ellipse, Paris, 1996.
- [TanHs30] : Tangente, Histoire des mathématiques de l'Antiquité à l'an Mil, HS n°30, Pole, Paris, 2007.


