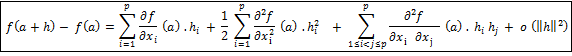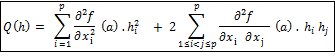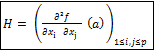Approche historique.
L'étude des extremum de fonctions de plusieurs variables commence en fait avec l'étude des formes quadratiques.
Les formes quadratique : pour plus de précision sur ce sujet ⇒ voir la page formes quadratiques.
Jean DIEUDONNE ([Dieudo]p64) considère qu'il n'y a pas véritablement de théorie algébrique des formes quadratiques au 18ème siècle (pas vraiment d'algèbre linéaire non plus).
En analyse, LAGRANGE Joseph Louis (1736-1813) étudie les extremums relatifs de fonctions à plusieurs variable.
Il construit une forme quadratique en réunissant les termes de dégré 2 dans le développement de TAYLOR de la fonction au voisinage du point.En dehors de cela, on ne rencontre au 18ème siècle que des formes quadratiques de 2 ou 3 variables. Avec les coniques et notamment la poursuite des travaux effectué par FERMAT Pierre de (1601-1665) , avec les quadriques étudiées par EULER(1707 - 1783) et avec les équations diophantiennes du second degré).
Etude des surfaces.
Le mathématicien français MONGE Gaspard (1746-1818). étudie les surface et dans son Application de l'analyse à la géométrie (avec Jean-Nicolas Hachette, 1807) il introduit la notion de ligne de courbure et les termes ellipsoïde, hyperboloïde et paraboloïde.
Dès 1801, il est le premier à utiliser systématiquement les équations aux dérivées partielles pour étudier les surfaces. [HaSu] p 245
La notion d'extremum. [Dieudo]p353
On arrive, vers la fin du 19ème siècle, à distinguer les notions d'extremum fort, correspondant à la notion de voisinage, et d'extremum faible. C'est avec le mathématicien français FRÉCHET Maurice (1878-1973) que ces notions reçoivent une formulation plus précise. Il publie à ce sujet, en 1906, son traité Sur quelques points du calcul fonctionnel.
Cours sur : Les extremums des fonctions numériques de plusieurs variables réelles. (Version PDF)
On considère une fonction f définie sur une partie U ⊂ IRp , à valeur dans IR.
![]()
1 – Définitions.
- La fonction f admet un maximum local en a ssi :
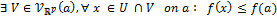
- La fonction f admet un minimum local en a ssi :
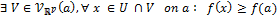
- La fonction f admet un maximum ou minimum local strict en a : idem avec des inégalités strictes.
- La fonction f admet un extremum local ou local strict en a si f admet un min, resp max…
- La fonction f admet un extremum global en a ssi :
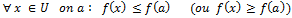
- a est un point critique de f ssi les dérivées partielles de f en a existent et sont nulles.
2 – Conditions nécessaires.
Théorème.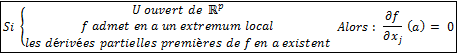
3 – Conditions suffisantes.
U ouvert de IRp et f C²(U).
3.a : Taylor Young ordre 2.
3.b : Théorème général : Cas des fonction de p variables réelles.
Soit a un point critique de f. On définit la forme quadratique définit sur
par :
La matrice hessienne H de Q dans la base canonique de IRp est :
3.b : Théorème pour les fonctions de 2 variables.
- Si Q est positive et non dégénérée ( soit si le spectre Sp(H) ⊂ IR+\{0} ), alors f admet un minimum local strict en a.
- Si Q est négative et non dégénérée ( soit si le spectre Sp(H) ⊂ IR-\{0}), alors f admet un maximum local strict en a.
- Si Q n’est ni positive, ni négative : alors pas d’extremum local en a.
On utilise les notations de MONGE, du nom du mathématicien français MONGE Gaspard (1746-1818).
- Si
alors f admet un minimum strict en a.- Si
alors f admet un maximum strict en a.- Si (s² - rt > 0) alors f n’admet pas d’extremum local en a.
On dit alors que f admet un point-selle (ou un point col en a)
4 - Exemples :
Exemple 1 : ![]() , f admet deux minimums locaux en A(1 ;-1) et B(-1 ;1)
, f admet deux minimums locaux en A(1 ;-1) et B(-1 ;1)
Exemple 2 : ![]() f admet un point selle en A(-2/3 ; 0)
f admet un point selle en A(-2/3 ; 0) 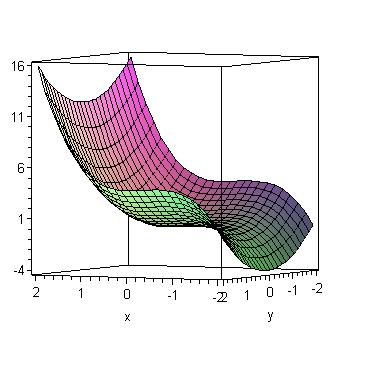
5 – Extremums globaux.
Proposition :
On a l'implication suivante